Schwingungsberechnung leicht gemacht
MIT DEM SCHWINGUNGSDIAGRAMM DEN GRAD DER ISOLIERUNG SELBER BESTIMMEN
Aufgabe der Schwingungsdämmung ist, eine Maschine so aufzustellen, dass keine unzulässige Schwingungen oder Stösse in die Umgebung gelangen. Theoretisch muss die Maschine so nachgiebig gelagert werden, dass sie sich unter dem Einfluss der beim Betrieb der Maschine auftretenden Massenkräfte nahezu frei bewegt. Durch Einsatz eines dauerelastischen Federsystems zwischen Maschine und Boden kann ein sehr guter Isolationswirkungsgrad erzielt werden. Allerdings muss bei einer überkritischen Lagerung das Federsystem eine Eigenfrequenz aufweisen, die wesentlich tiefer ist als die Störfrequenz.
Das unten abgebildete Diagramm ermöglicht auf einfache Weise die Bestimmung der Einfederung, die zur Erzielung der gewünschten Isolierung notwendig ist. Allerdings ist die dauerhafte Veränderung der Störfrequenz nur möglich, wenn die Feder auch dauerhaft elastisch bleibt. Nur Materialien, die sich nicht verdichten oder zusammenpressen lassen, d.h. unter ständiger dynamischer Beanspruchung sich nicht setzen, bieten Gewähr für den angegeben Wirkungsgrad.
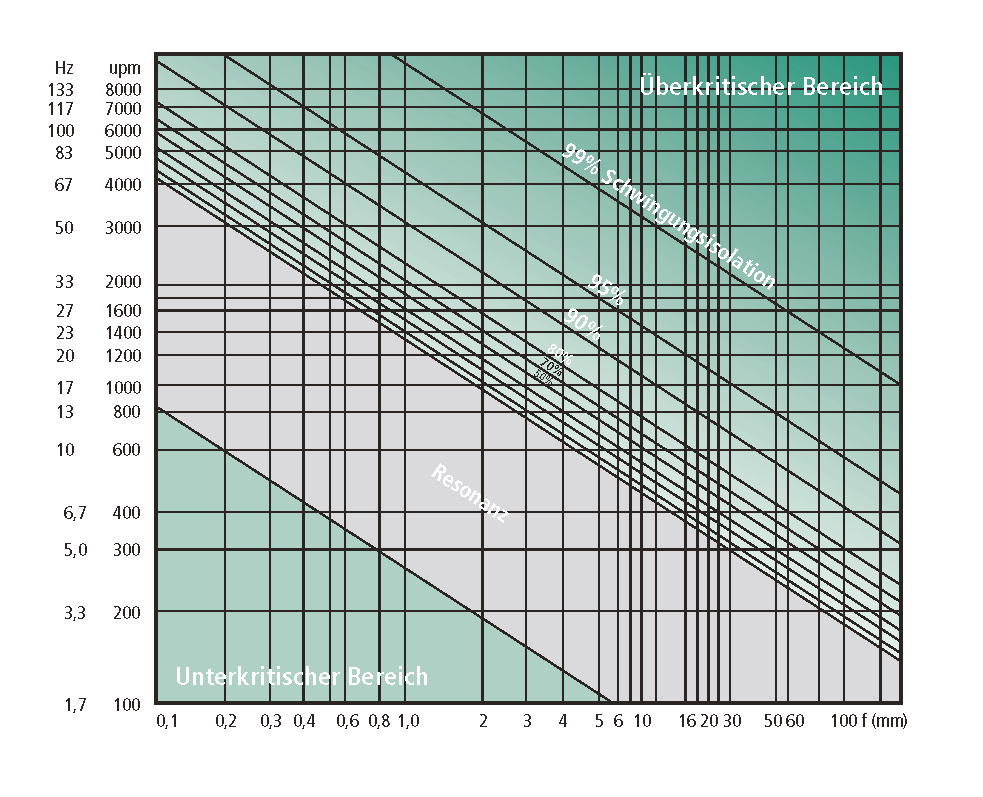
ISOLATIONSDIAGRAMM
Selbstverständlich gilt dieses Diagramm nur für Maschinen die eine gleich bleibende Leistung aufweisen. Weiche Lagerungen sind allerdings nicht risikolos einsetzbar. Nicht alle Maschinen ertragen Eigenbewegungen und benötigen deshalb zur Isolation zumindest eine Dämpfung. Auch verlangen viele Maschinen eine Stabilität die mit weichen Federn nicht zu erreichen ist. Dem Anwender stehen aber eine Vielzahl von weiteren Möglichkeiten wie Reflexionsdämmung (im Katalog) oder sogenannte unterkritische Lagerungen zur Verfügung. Nicht zu unterschätzen ist der Standort der Maschine. Die Eigenfrequenz des Bodens kann für eine Isolation entscheidend sein. So ist der Unterschied eines Maschinenstandortes im Stockwerk zu einem festen Fundamentboden enorm. Nochmals andere Resultate lassen sich mit Fundamentisolierungen erzielen. Lassen Sie sich von uns beraten, wir arbeiten Ihnen gerne eine zufrieden stellende Lösung aus.
Grundlage dieses Diagramms ist die mathematische Beziehung
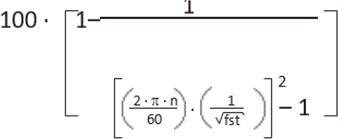
n = Störfrequenz (min-1)
fst = statische Einfederung (mm)
Resonanz entsteht, wenn Eigenfrequenz und Störfrequenz gleich gross sind. Das System schaukelt sich auf und kann Schaden nehmen.
Beispiel: Eine Stanze führt pro Minute 1600 Hübe aus. Die Schwingungen sollen zu 80% vom Gebäude ferngehalten werden. Im Diagramm (Störfrequenz 1600 Upm) fährt man horizontal bis zur schrägen Übertragungslinie 80%. Im Schnittpunkt fährt man vertikal nach unten und findet die notwendige Einfederung von 2 mm.


